An Abundance of K3 Fibrations from Polyhedra with Interchangeable Parts (by Philip Candelas, Andrei Constantin, Harald Skarke),which is purely mathematical – it is a paper about higher-dimensional shapes – but its relevance for high-energy physics is obvious. Philip Candelas in particular is a pioneer of the applications of Calabi-Yau manifolds in string theory. He's also highly active these days. Aside from the newest paper, you may be interested in a paper from December 2011 in which they construct a heterotic string model that produces the MSSM with three generations and absolutely nothing else at low energies!
The today's paper is dedicated to the memory of Maximilian Kreuzer († November 2010) of Vienna who has done lots of work and let me say that I haven't seen a more original work dedicated to a recently deceased person for quite some time.
Let me begin at a natural starting point.
Quantum field theories (and more primitive theories) require that you choose the spacetime dimension at the beginning. This number is a "metaphysical assumption", something you shouldn't think about. At most, you may invent anthropic stories unrelated to QFT that explain how difficult life could be in a higher number of dimensions than those 3+1 dimensions (space+time) that we observe.
But string theory is a theory of everything so it dictates what the number of spacetime dimensions may be or must be. In perturbative superstring theory, the spacetime has to have 9+1 dimensions in total. It implies that there are 6 hidden dimensions of spacetime we don't know. Similarly, in M-theory, there have to be 7 hidden dimensions and in F-theory, there are 8 of them even though 2 of them are predestined to remain infinitely small.
(See Where are we in extra dimensions and other articles for a basic sketch of shapes of extra dimensions in string theory.)
The shape of the extra dimensions may be studied separately from the large 3+1 dimensions we know. This statement is pretty much equivalent to saying that the total 10-, 11-, or 12-dimensional spacetime has the shape given by the Cartesian product\[
{\mathcal M}_{\rm total} = {\mathcal M}^{3+1} \times CY.
\] The letters \(CY\) indicate the shape of hidden or extra dimensions. I said that the spacetime dimension isn't arbitrary in string theory. Even when we choose one of the few possibilities for the spacetime dimension, the shape isn't arbitrary, either. The shape has to obey the equations of string theory, too. When the shape is large enough and/or when one may argue that corrections may be dropped or neglected, the equations of string theory for the shape reduce to Einstein's equations. In the vacuum, they may be written as\[
R_{\mu\nu} = 0.
\] The Ricci curvature tensor vanishes. This condition is a priori valid for the total spacetime. However, under various sensible conditions, it is equivalent to the Ricci-flatness of the compact manifold \(CY\) itself. The hidden dimensions have to obey Einstein's equations of the general theory of relativity. And they're very constraining.
One class of solutions are flat manifolds. They have no curvature; the Riemann curvature tensor vanishes so the Ricci tensor vanishes, too. The infinite flat space is an example but it is phenomenologically excluded; we just don't observe many new flat infinitely large dimensions and we don't observe spin-1 partners of all known fermions etc. However, you may also construct flat compact (i.e. finite-volume) manifolds by making the coordinates periodic. We call these compactifications (specified by a lattice of periodicities, not necessarily "simple periodicity" for each individual coordinate) toroidal compactifications.
Toroidal compactifications are therefore an important and simple enough class of solutions to the equations determining the shape of extra dimensions. For a given dimension of the torus, we may still choose its 6-8 radii and the "angles" in between them. These toroidal compactifications usually preserve all the supersymmetries of the parent, higher-dimensional theory which implies that the spectrum is too organized and simple – more so than the particle spectrum in the real world.
Are there other solutions?
Yes, you may also take "orbifolds" of the tori. But these shapes strictly speaking have a nonzero delta-function-like Riemann tensor at the fixed points of the orbifold action (which is used to identify points to build the orbifold: an orbifold is a coset or quotient or a set of equivalence classes). However, it may be shown that the orbifolds are rather generally just special points in broader moduli spaces of shapes that have nonzero curvature everywhere (although there may be many different ways to describe the same points and it may be debatable which of them is more fundamental if any).
So what are the non-flat but Ricci-flat shapes?
Let's look at them according to their dimension. One-dimensional manifolds are locally a line which can't have a curvature so as long as they remain non-singular, there is nothing else to discuss. An infinite line and a circle are the only two closed one-dimensional manifolds.
Closed two-dimensional orientable manifolds may be visualized as genus \(h\) Riemann surfaces – a sphere with \(h\) handles attached to it. The integral of the Ricci curvature scalar over the surface is proportional to \[
\chi = 2 - 2h.
\] The number \(\chi\) – which is pronounced as "chi" – is known as the Euler character. If you approximate a surface by a polyhedron, you may calculate \(\chi\) as the number of vertices minus the number of edges plus the number of two-dimensional faces minus the number of three-dimensional faces (for higher-dimensional objects) plus minus plus minus, you get the point.
At any rate, if the Ricci tensor is zero everywhere, it is obvious that \(2-2h\) must be zero, too. So \(h=1\) and the sphere with one handle is nothing else than the two-dimensional torus. It's the only two-dimensional Ricci-flat manifold. Its shape may be specified by a complex number \(\tau\) and all values of \[
\tau' = \frac{a\tau +b}{c\tau +d},\quad ad-bc=1
\] give the same shape. This equivalence is known as an \(SL(2,\ZZ)\) symmetry. Fine. We have already mentioned that tori are simple solutions to Einstein's equations and we returned to them again. I won't do it again. Instead, I just say that \(n\)-dimensional tori exist and are Ricci-flat for every positive integer \(n\); the value may be odd and for \(n=1\), they are known as circles.
What about the other solutions? It turns out that there are many new Ricci-flat manifolds you may construct with the help of complex numbers – by pairing the real coordinates on the manifold into complex coordinates. That means that we obtain new non-flat but Ricci-flat manifolds in (real) dimensions 2,4,6, and so on. In these interesting classes of shapes (and their vicinity), the Ricci flatness condition becomes equivalent to a reduced "holonomy group" (\(SU(2),SU(3),G_2,SU(4),\dots\)) or to some supersymmetry that may be preserved despite the curvature (because there exist "Killing spinors" on the manifold).
An IQ test: What is the next dimension after 2,4,6 for which you may obtain very nice, new, non-flat but Ricci-flat, and in fact supersymmetric manifolds? What is the next number after 2,4,6? Yes, it is 7. :-) Algebraic geometry has the right to be more subtle than kindergarten mathematics! The new 7-dimensional manifolds are those of a \(G_2\) holonomy – the rotations of the tangent space induced by round trips form a group isomorphic to the exceptional automorphism group of the octonions \(\OO\). We will avoid this exceptional case in the rest of this text.
Fine. So I promised you new nontrivial non-flat but Ricci-flat manifolds whose dimension is 4 and 6. In the case of 4, the only new solution (when it comes to the topology) is the so-called K3 manifold.
A two-dimensional visualization above captures a manifold whose topology is completely fixed. There are \(19\times 3\) real parameters that may be adjusted to change the detailed shape of the manifold. That's it. In the article linked above, I described K3 as the simplest possible compactification of extra dimensions after the tori. And this simplicity – and, aside from the tori, uniqueness among the 4-real-dimensional manifolds – implies that the K3 manifold is important in the broader scheme of things, too.
The new paper I want to discuss uses the K3 manifolds in a very important way, too.
Now, let us jump to 6 extra dimensions. That's the first example directly relevant for phenomenology in particle physics. It's because superstring theories have 10 spacetime dimensions so 6 of them have to be compactified to preserve 4 large dimensions we know. In particular, compactifications of heterotic string theory on six-dimensional Calabi-Yau manifolds \(CY\) represented the first realistic class of the Universe around us within string theory. By Calabi-Yau manifolds, we mean special 6-real-dimensional manifolds that preserve some supersymmetry (and therefore Ricci-flat) which are neither \(T^6\) nor \(T^2\times K3\), i.e. neither a six-torus nor the product of a two-torus and a K3 manifold.
Their unusually realistic structure was discovered in a 1985 paper by Candelas, Strominger, Horowitz, and Witten. Yes, it's the same Candelas. A natural question to ask was: What is the shape of the extra dimensions, \(CY\)? Andy Strominger was assigned his task. He went to math libraries and found exactly one example, the quintic hypersurface in a complex projective space. That was great: they apparently had the unique theory of everything. You can't be shocked that Edward Witten would offer the estimate of a "few weeks" for the time needed to calculate the muon mass and all other parameters and complete the quest for a TOE. It was a reasonable guess; we just know today that it was wrong, too.
Why was it wrong? Well, tens of thousands of six-dimensional Calabi-Yau spaces – manifolds that are not flat but that manage to be Ricci-flat by preserving 1/4 of the supersymmetries as well – were later found.
The most versatile class of Calabi-Yau manifolds are obtained from the so-called reflexive polytopes (higher-dimensional polyhedra; "reflexive" refers to the usual duality for polytopes) by the Batyrev construction. (This particular machinery is much more well-known to trained mathematicians than trained physicists, of course. Some of its insights overlap with discoveries that were made by physicists, using the physics jargon and the physical intuition.) Max Kreuzer had intensely worked on these things. He listed all the 473,800,776 such polytopes. Again, if physics with a larger number of solutions looks hopelessly hard to you, it is probably just your problem. Here we are talking about less than half a billion of shapes. It's easy to list them – the number is thousands of times smaller than the Greek government's debt.
One may obtain Calabi-Yau manifolds from these polytopes. The most characteristic integer label describing the topology of a manifold is the Euler character \(\chi\) I have already mentioned (think about the vertices, edges, faces, and so on as the most general definition). For Calabi-Yau manifolds, the Euler character may also be calculated as\[
\chi = 2(h^{1,1}-h^{1,2})
\] where \(h^{1,1}\) and \(h^{1,2}\) are the so-called Hodge numbers, the numbers of two-dimensional and three-dimensional cycles (topologically nontrivial, topologically inequivalent, and independent submanifolds of these dimensions: the two indices label holomorphic and antiholomorphic dimensions separately but I don't want to go into that here). The Euler character is always drawn on the \(x\)-axis of the plots known as the Hodge plots. The other coordinate \(y\) is defined to be the "height" \(h^{1,1}+h^{1,2}\) in almost all cases.
Here is the basic Hodge plot of the known Calabi-Yau manifolds: 30,108 distinct points i.e. pairs \( (h^{1,1},h^{1,2}) \) are included on the picture. That means that there are at least 30,108 known Calabi-Yau topologies (but if the two integers don't specify the topology of a manifold uniquely, there may be many more and the new paper talks about 700,000+ Calabi-Yaus, too).

Click to zoom in.
You may see that the number of topologies is large but at this moment, it seems reliably finite. The Euler character only goes from \(\chi=-960\) to \(\chi=+960\) and if you think about the patterns on the picture above, you may quickly decide that it is not an accident.
What patterns do you see on the Hodge plot above? First of all, it is left-right-symmetric. This picture makes it obvious that the corresponding symmetry is called "mirror symmetry" – one of the remarkable mathematical relationships that probably wouldn't have been discovered at all if people didn't know string theory.
While the left-right symmetry looks trivial on such a plot, you must realize that it is an incredibly complicated map. For example, take the manifolds in the right upper and left upper corners, the mirror pair \({\mathcal M}_{11,491}\) and \({\mathcal M}_{491,11}\). They're "extreme" in some sense, coming from the most complex polytopes. You may imagine that these manifolds are some sort of ancestors, Adam and Eve. Adam has 11 hair and 491 legs while Eve has 491 hair and 11 legs only. Their shapes are completely different but the existence of one of them guarantees the existence of the other. And in fact, string theory compactified on one of them produces the same physics as (the same or different) string theory compactified on the mirror partner.
However, if you look carefully, you will realize that the map\[
\chi\to -\chi
\] isn't the only apparent symmetry in the Hodge plot. And they did notice it wasn't the only one. The image also seems to have two valleys, a left valley and a right valley, and they're left-right symmetric by themselves. Alternatively, you may combine this left-right reflection with the original \(\chi\to-\chi\) reflection to get a translation\[
(\chi, y) \to (\chi+960,y).
\] The Hodge numbers jump by \(\pm 240\) if you care. That's quite a clear symmetry of many (but not all) points in the Hodge plot and you may ask what's the reason behind this symmetry.
And the authors have understood it. The Calabi-Yau manifolds represented by these points can actually be constructed from polytopes that may be cut into two pieces, top and bottom, or X and Y chromosomes if you prefer my terminology. As long as the boundary between the two chromosomes goes along a K3 fibration – a manifold that may be visualized as a K3 surface (see above) attached to every point of a base manifold, i.e. a Cartesian product in which the shape of the K3 may change and rearrange as we move along the base manifoold – the two chromosomes are independent and in fact, genetic engineering is allowed. You may combine different X chromosomes with different Y chromosomes. One may say that the change of the Euler character corresponds to the replacement of the "simplest" top by the "most complicated one".
The paper contains several such constructions that explain many patterns of this sort. I recommend you to open the paper and look at least at the pictures – various colored versions of the simple Hodge plot above – because they're pretty. The Calabi-Yau manifolds are genetically decomposed to pairs of chromosomes and slices and projections involving K3 fibers play an important role. Moreover, the K3 fibrations may be classified by Lie group labels. So there exist things such as \(E_8\times \{1\}\) fibrations and \(E_7\times SU(2)\).
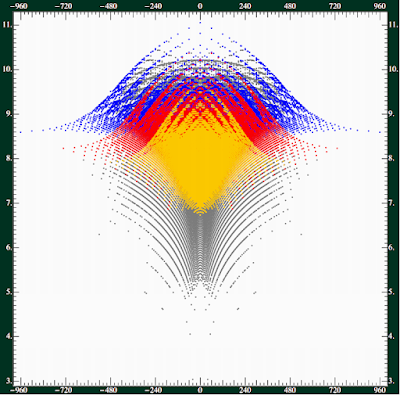
Click to magnify the Hodge fountain.
I couldn't resist to include at least one more picture from their paper. The \(x\)-axis shows the \(\chi\) once again while \(y=\ln (h^{1,1}h^{1,2})\). The blue, red, and yellow points show K3 fibrations of the \(E_8\times SU(1)\), both, and \(E_7\times SU(2)\) type, respectively. You may say that the \(E_8\times SU(1)\) are the "more rare" points near the top – such as Adam and Eve – while the more "generic" Calabi-Yau manifolds divide the maximum group \(E_8\) more evenly.
There are many more relationships and genetic engineering operations mentioned in the paper. They explain lots of visual observations about the picture you could make even without the knowledge of any algebraic geometry – or any advanced maths, for that matter. The number of different relationships between the Calabi-Yau shapes – e.g. various kinds of ancestry – is large. In a sense, it shouldn't be surprising. There are many ways to cut, glue, mill, drill, project [and many more verbs] three-dimensional objects. The six-dimensional engineers have many more verbs that describe what they can do with "shapes" in their factories. ;-) But don't misinterpret this "factory" jargon: the operations discussed here are much more natural and much less "man-made".
At the end, the number of Calabi-Yaus that are left unmatched to others by these operations and relationships is very small. And as I have said many times over the years, these operations and relationships between different shapes (and perhaps between different decorated shapes that also contain branes, fluxes, and everything else that string theory allows to be nontrivial) may be more than just mathematical curiosities or tools to construct various structures. Some of them may be crucial in cosmological mechanisms that one must understand to master the vacuum selection problem.
The membrane nucleation and tunneling on the landscape was often compared to some kind of "mutation" in a reproductive tree of universes – a tree implied by eternal inflation. But it's plausible that the Calabi-Yaus may choose their X,Y chromosomes (top and bottom) kind of separately, that there is a "sexual reproduction" of universes with newer Calabi-Yaus.
Effectively, some of the "reducible shapes" or "shapes that are distant descendants of others" may be favored or disfavored (or unstable). Also, when you try to calculate the probability that different shapes are realized in Nature, it's plausible that there is some mechanism that favors the individual chromosomes separately. For example, it seems "almost obvious" to me that Nature either heavily favors the shapes near the top of the fountain – the \(E_8\times SU(1)\) types – or those near the bottom. It's plausible that there exists a simple enough – and perhaps even justifiable (by arguments we would already agree with) – rule that will allow physicists to pick the right (or much more likely to be right) shapes sometimes in the future.
And that's the memo.
0 comments:
Post a Comment