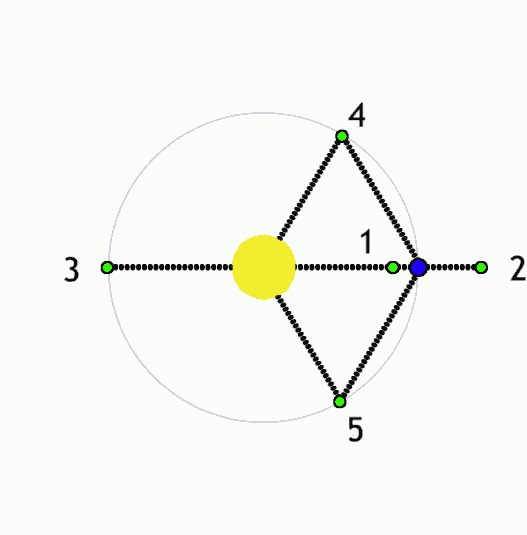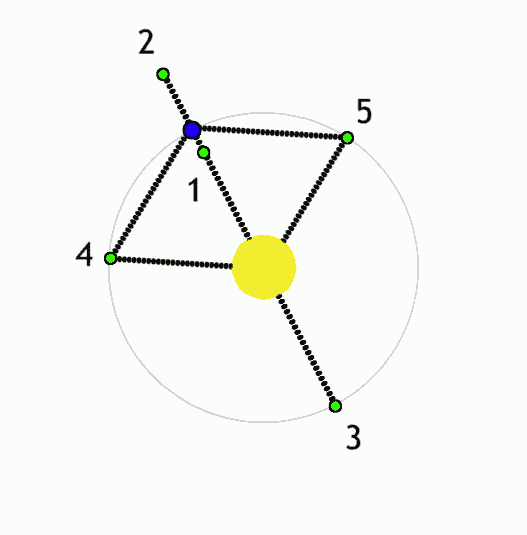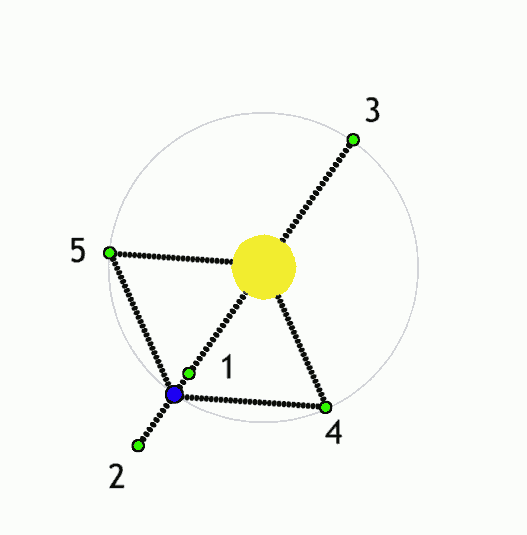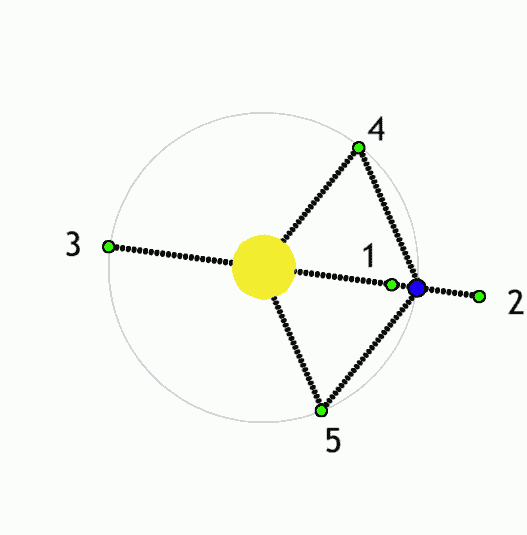
Yellow is the Earth, blue is the Moon. And 1,2,3,4,5 are the Lx Lagrange points.
Instead of resembling the International Space Station that orbits the Earth just 400+ km above the surface (see current location to check whether you may see the dot above you), it would be placed in a more exotic place – the Earth-Moon L2 Lagrange point.
The point is located about 60,000 km behind the Moon so you can't see it from the Earth. I said "it is located". When is it located? The funny feature of the Lagrange points is that if you place something at a Lagrange point – defined by its position relatively to two celestial bodies that orbit each other – it stays there. It stays there from the viewpoint of the rotating reference frame which keeps the orbiting plane as well as the locations of the two celestial bodies fixed.
You see that there are five Lagrange points for each pair; L4 and L5 form a mirror pair. L2 is behind the Moon and has the same angular frequency as the Moon – so it has a higher velocity. Consequently, the centifugal acceleration \(v\omega\) is greater than the Moon's, but that's OK because the attractive acceleration is also greater than the acceleration that attaches the Moon to the Earth: the Moon itself adds its own force.
Note that the L2's distance from the Earth is about \(7/6\) times the distance of the Moon, so the centrifugal acceleration \(v\omega\) is about \(7/6\) times greater than it is for the Moon. The Earth's attractive acceleration is \((7/6)^2\) times smaller than for the Moon, because of the inverse square law, but\[
\zav{\frac 67}^2 + \frac{1}{81}\cdot 6^2\sim 1.18\sim \frac 76
\] which gives approximately the right enhancement, with the help of the term from the Moon which is suppressed by Moon's \(81\) times smaller mass but enhanced by the \(6\) times shorter distance from the Moon.

An Orion capsule (picture above) could be sent over there by the Space Launch System between 2017 and the 2020s so don't change your dinner plans yet. A particular plan suggests the first people at L2 around 2021. They would be the first people who would have the privilege of seeing no Earth around them for extended periods of time. :-) Instead, they would be watching the other side of the (six times larger than usual) Moon than almost all other mortals. Note that the Earth's radius is just \(3.66\) times larger than Moon's but the Earth is six times further from L2 than the Moon, so it's too small to be seen behind the Moon.

Solar activity from planetary tidal forces
Incidentally, I am kind of fascinated by the new paper (via WUWT) showing a rather remarkable agreement in the Fourier transformation of two charts.
One of them is the solar activity, as reconstructed from some cosmogenic radionuclides (geology), and the other one is a theoretical model calculating the tidal forces of all the planets on the Sun's tachocline. The agreement in the precise frequencies of the peaks looks totally remarkable. A priori, I would think that the tides are too weak. On the other hand, many things may be strengthened by various effects and because it's a real measurable effect now, tides scaling as the justifiable, measurable yet modest \(1/r^3\), and not a hypothetical effect of the relative position of the barycenter and the Sun which would contradict the equivalence principle, none of my criticisms against the "barycenter theories" apply.
Even if this planetary influence on the solar activity is genuine, it doesn't imply that either of these curves is a good proxy to the Earth's climate. But the picture looks rather intriguing... Needless to say, it's rather compatible with the 30 years of warming in the recent era and it predicts some cooling for the following decades (see e.g. Figure 3 in the paper).
No comments:
Post a Comment